Расшифровать шифр
Содержание
10 популярных кодов и шифров
Необходимость засекречивать важные послания возникла еще в древности. Со временем люди находили новые, все более сложные способы делать послания недоступными чужим глазам. Вопреки распространенному мнению, код и шифр — это не одно и то же.
В коде каждое слово заменяется на какое-то иное кодовое слово, в то время как в шифре заменяются сами символы сообщения. Когда люди говорят «код», они, как правило, имеют в виду «шифр». Древние рукописи и языки были поняты с помощью техник декодирования и дешифрования.
Самый известный пример — Розеттский камень Древнего Египта. Фактически коды и шифры определяли исход многих войн и политических интриг на протяжении всей истории человечества.
Существуют тысячи типов шифрования сообщений, но в этой статье мы рассмотрим лишь 10 самых известных и значимых из них.
10. Стеганография
Стеганография — это искусство скрытого письма. Этой технике даже больше лет, чем кодам и шифрованию. Например, сообщение может быть написано на бумаге, покрыто ваксой и проглочено с той целью, чтобы незаметно доставить его получателю. Другой способ — нанести сообщение на бритую голову курьера, подождать, пока волосы вырастут заново и скроют послание.
Лучше всего для стенографии использовать повседневные объекты. Когда-то в Англии использовался такой метод: под некоторыми буквами на первой странице газеты стояли крохотные точки, почти невидимые невооруженным глазом.
Если читать только помеченные буквы, то получится секретное сообщение! Некоторые писали сообщение первыми буквами составляющих его слов или использовали невидимые чернила. Была распространена практика уменьшения целых страниц текста до размера буквально одного пикселя, так что их было легко пропустить при чтении чего-то относительно безобидного.
Стенографию лучше всего использовать в сочетании с другими методами шифрования, так как всегда есть шанс, что ваше скрытое послание обнаружат и прочитают.
9. ROT1
Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, A заменяется на B, B на C, и т.д. «ROT1» значит «ROTate 1 letter forward through the alphabet» (англ. «сдвиньте алфавит на одну букву вперед»).
Сообщение «I know what you did last summer» станет «J lopx xibu zpv eje mbtu tvnnfs». Этот шифр весело использовать, потому что его легко понять и применять, но его так же легко и расшифровать. Из-за этого его нельзя использовать для серьезных нужд, но дети с радостью «играют» с его помощью.
Попробуйте расшифровать сообщение «XBT JU B DBU J TBX?».
8. Транспозиция
В транспозирующих шифрах буквы переставляются по заранее определенному правилу. Например, если каждое слово пишется задом наперед, то из «all the better to see you with» получается «lla eht retteb ot ees joy htiw». Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет «la tl eh eb tt re ot es ye uo iw ht».
Подобные шифры использовались в Первую Мировую и Американскую Гражданскую Войну, чтобы посылать важные сообщения. Сложные ключи могут сделать такой шифр довольно сложным на первый взгляд, но многие сообщения, закодированные подобным образом, могут быть расшифрованы простым перебором ключей на компьютере. Попробуйте расшифровать «THGINYMROTSDNAKRADASAWTI».
7. Азбука Морзе
В азбуке Морзе каждая буква алфавита, все цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов, часто называемых «точками и тире». Так, A — это «•–», B — «–•••», и т.д.
В отличие от большинства шифров, азбука Морзе используется не для затруднения чтения сообщений, а наоборот, для облегчения их передачи (с помощью телеграфа). Длинные и короткие сигналы посылаются с помощью включения и выключения электрического тока.
Телеграф и азбука Морзе навсегда изменили мир, сделав возможной молниеносную передачу информации между разными странами, а также сильно повлияли на стратегию ведения войны, ведь теперь можно было можно осуществлять почти мгновенную коммуникацию между войсками.
6. Шифр Цезаря
Шифр Цезаря называется так, как ни странно, потому что его использовал сам Юлий Цезарь. На самом деле шифр Цезаря — это не один шифр, а целых двадцать шесть, использующих один и тот же принцип! Так, ROT1 — всего один из них. Получателю нужно сказать, какой из шифров используется.
Если используется шифр «G», тогда А заменяется на G, B на H, C на I и т.д. Если используется шифр «Y», тогда А заменяется на Y, B на Z, C на A и т.д. На шифре Цезаря базируется огромное число других, более сложных шифров, но сам по себе он не представляет из себя интереса из-за легкости дешифровки.
Перебор 26 возможных ключей не займет много времени. Li bra ghflskhu wklv dqg bra nqrz lw, fods brxu kdqgv.
5. Моноалфавитная замена
ROT1, азбука Морзе, шифр(ы) Цезаря относятся к одному и тому же типу шифров — моноалфавитной замене. Это значит, что каждая буква заменяется на одну и только одну другую букву или символ. Такие шифры очень легко расшифровать даже без знания ключа. Делается это при помощи частотного анализа.
Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».
Человек, расшифровывающий моноалфавитный шифр, может смотреть на частоту встречающихся букв и почти законченные слова. Так, «T_E» с большой долей вероятности окажется «ТНЕ». К сожалению, этот принцип работает только для длинных сообщений.
Короткие просто не содержат в себе достаточно слов, чтобы с достаточной достоверностью выявить соответствие наиболее часто встречающихся символов буквам из обычного алфавита.Мария Стюарт использовала невероятно сложный моноалфавитный шифр с несколькими вариациями, но когда его наконец-то взломали, прочитанные сообщения дали ее врагам достаточно поводов, чтобы приговорить ее к смерти. Ptbndcb ymdptmq bnw yew, bnwzw raw rkbcriie wrze bd owktxnwa.
4. Шифр Виженера
Этот шифр сложнее, чем моноалфавитные. Представим, что у нас есть таблица, построенная по тому же принципу, что и приведенная выше, и ключевое слово, допустим, «CHAIR».
Шифр Виженера использует тот же принцип, что и шифр Цезаря, за тем исключением, что каждая буква меняется в соответствии с кодовым словом.
В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова (в нашем случае «С»), вторая буква — согласно алфавиту для второй буквы кодового слова («H»), и так далее.
В случае, если послание длиннее кодового слова, то для (k*n+1)-ой буквы (где n — это длина кодового слова) вновь будет использован алфавит для первой буквы кодового слова, и так далее. Очень долгое время шифр Виженера считался невзламываемым.
Чтобы его расшифровать, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания, где n — предполагаемая длина кодового слова. Если длина была угадана верно, то и сам шифр вскроется с большей или меньшей долей вероятности. Если предполагаемая длина не дает верных результатов, то пробуют другую длину кодового слова, и так далее до победного конца. Eoaqiu hs net hs byg lym tcu smv dot vfv h petrel tw jka.
3. Настоящие коды
В настоящих кодах каждое слово заменяется на другое. Расшифровывается такое послание с помощью кодовой книги, где записано соответствие всех настоящих слов кодовым, прямо как в словаре.
Преимущества такого способа в том, что сообщению необходимо быть ЧРЕЗВЫЧАЙНО длинным, чтобы можно было его взломать с помощью частотного анализа, так что коды полезнее некоторых шифров. Многие страны использовали коды, периодически их меняя, чтобы защититься от частотного анализа.
Тем не менее, есть и минус: кодовая книга становится критическим предметом, и в случае, если она будет украдена, то с ее помощью больше будет невозможно что-либо зашифровать, и придется придумывать новый код, что требует огромных усилий и затрат времени.Обычно коды используют только богатые и влиятельные люди, которые могут поручить работу по их составлению другим.
2. Шифр Энигмы
Энигма — это шифровальная машина, использовавшаяся нацистами во времена Второй Мировой. Принцип ее работы таков: есть несколько колес и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.
Соль в том, что существовало более ста триллионов возможных комбинаций колес, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения. Все Энигмы были идентичными, так что при одинаковом начальном положении колес на двух разных машинах и текст выходил одинаковый.
У немецкого командования были Энигмы и список положений колес на каждый день, так что они могли с легкостью расшифровывать сообщения друг друга, но враги без знания положений послания прочесть не могли. Когда Энигма попала в руки к союзникам, они все равно сперва не могли ничего с ней сделать, потому что не знали положений-ключей.
Дело по взлому шифра Энигмы было начато в польской разведке и доведено до конца в британской с помощью ученых и специальных машин (например, Turing Bombe, чья работа заключалась в том, чтобы моделировать одновременно работу сразу нескольких десятков Энигм).
Отслеживание коммуникаций нацистов дало армии союзников важное преимущество в войне, а машины, использовавшиеся для его взлома, стали прообразом современных компьютеров.
1. Шифрование публичным ключом
Алгоритм шифрования, применяющийся сегодня в различных модификациях буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это некое очень большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ.
Например, публичный ключ — это 1961, а секретный — 37 и 53. Открытый ключ используется для того, чтобы зашифровать сообщение, а секретный — чтобы расшифровать. Без секретного ключа расшифровать сообщение невозможно.
Когда вы отправляете свои личные данные, допустим, банку, или ваша банковская карточка считывается банкоматом, то все данные шифруются открытым ключом, а расшифровать их может только банк с соотвествующим секретным ключом. Суть в том, что математически очень трудно найти делители очень большого числа. Вот относительно простой пример.
Недавно RSA выделила 1000 долларов США в качестве приза тому, кто найдет два пятидесятизначных делителя числа 1522605027922533360535618378132637429718068114961380688657908494580122963258952897654000350692006139.
Перевод статьи «10 codes and ciphers»
Александр Курилкин
Источник: https://tproger.ru/translations/10-codes-and-ciphers/
Стойкие шифры

Обычные шифры из детективных романов часто устроены так: каждая буква сообщения заменяется каким-нибудь определённым значком или другой буквой. Подобные шифры очень ненадёжны, и вот почему.
Буквы в текстах на русском языке (да и на любом языке вообще) встречаются неравномерно. Например, буква «О» в русских текстах встречается чаще всех других букв, а буква «Ъ» — реже всего.
У каждой буквы есть своя примерная частота появления в тексте (смотри таблицу на поле справа).
Сочетания букв тоже встречаются неравномерно (например, «ьь» вообще не встречается). Конечно, все эти частоты зависят от конкретного текста — скажем, в биологической статье о жужелицах буква «ж» явно будет встречаться чаще, чем обычно. Но приведённая таблица вполне годится как ориентир.
Так вот, описанный способ шифровки не изменяет частот — просто теперь с аналогичной частотой будет появляться не сама буква, а заменяющий её значок. Высчитав частоту появления каждого значка в шифровке и сравнив полученные данные с таблицей частот, мы можем сделать предположения, какой букве какой значок соответствует.
Далее пробуем заменять значки один за одним на буквы, проверяя свои догадки, корректируя их и делая новые, и постепенно расшифровываем текст. Если он не слишком короткий, мы с большой вероятностью его полностью расшифруем (хотя это может оказаться не совсем простым делом). Кстати, намного чаще любой буквы встречается пробел, разделяющий слова.
Поэтому если пробел используется в шифровке и тоже заменён на какой-то значок, мы разгадаем его в первую очередь.
Совершенный шифр
Опишем теперь шифр, который принципиально не поддается расшифровке без знания ключа.
Сопоставим каждой букве русского алфавита свою последовательность из 0 и 1 длины 5 (пятизначный двоичный код), например: А — 00000, Б — 00001, В — 00010 и так далее (или в каком-то другом порядке).
Если буквы Е и Ё кодировать одинаково, то последовательностей как раз хватит (их 32, а в алфавите 33 буквы).
Заменим в тексте каждую букву на её двоичный код, получим последовательность из 0 и 1 (двоичный текст). Это пока ещё не шифровка — мы бы легко разгадали, какая буква на какую последовательность заменена (тем же методом, что и в случае замены букв на значки).Чтобы зашифровать полученный двоичный текст, нам потребуется ещё ключ — случайная последовательность из 0 и 1 такой же длины. Этот ключ должен быть и у отправителя шифрованного сообщения, и у адресата.
Для зашифровки просто складываем две последовательности нулей и единиц — двоичный текст сообщения и ключ: первую цифру с первой, вторую со второй, и так далее. Но складываем по особым правилам:
0 + 0 = 0, 1 + 0 = 1, 0 + 1 = 1, 1 + 1 = 0
(в математике это называется сложением по модулю 2).
Полученная последовательность и будет зашифрованным сообщением. Чтобы расшифровать её, надо просто… снова прибавить к ней ключ! Тогда мы как бы прибавим к исходной последовательности ключ два раза. А по нашим правилам, прибавляя две одинаковые цифры мы ничего не меняем, то есть мы вернёмся к исходному двоичному тексту. Схематически процесс шифрования и дешифрования можно описать так:
текст + ключ = шифровка;
шифровка + ключ = текст + ключ + ключ = текст.
Ясно, что расшифровать сообщение, не зная ключа, невозможно. Нам как бы дана сумма двух чисел, и нельзя восстановить одно из слагаемых, ничего не зная про другое. Имея на руках лишь шифровку, мы знаем только, что исходный текст может быть абсолютно любым текстом соответствующей длины. Ведь по любому такому тексту можно изготовить ключ, который приведёт ровно к той же самой шифровке!
Недостаток описанного способа в том, что каждый текст требует нового ключа такой же длины — если повторять ключи, появляется возможность расшифровки. Например, мы могли бы попробовать вместо длинного ключа использовать ключ всего из пяти символов, скажем 11010. Разбиваем двоичный текст на пятёрки цифр и прибавляем к каждой пятёрке 11010.
Фактически, мы просто заменяем каждую пятёрку цифр на какую-то другую фиксированную пятёрку. В этом случае расшифровать исходный текст так же легко, как если бы мы просто заменили его двоичным кодом, не прибавляя никакого ключа.
Использовать длинные ключи, но всё же существенно более короткие, чем текст, тоже опасно — есть метод определения длины ключа, а после того как длина ключа установлена, можно применить частотный анализ.
Поэтому надо заготовить ключ огромной длины заранее и лишь указывать, например, в начале шифровки, какое место ключа используется. При этом очень важно, чтобы ключ был случайной последовательностью из 0 и 1.Например, последовательности 11111111111111111 и 010101010101010 не случайные. Кстати, придумать случайную последовательность не так-то просто.
Трудно даже (но возможно) дать чёткое определение, какие последовательности могут считаться случайными.
Немного истории и литературы
Подобный шифр использовал Макс Кристиансен-Клаузен, шифровальщик выдающегося советского разведчика Рихарда Зорге.
Наиболее часто употребляемые буквы английского алфавита s, i, o, e, r, a, t, n заменялись цифрами от 0 до 7, а остальные буквы — числами от 80 до 99 (чтобы не возникало путаницы, когда числа записывались подряд).
Ключом служили старые выпуски «Статистического ежегодника Германского рейха» с множеством числовых данных. Ключ записывали под текстом и прибавляли, причём если сумма двух цифр превышала 10, то записывалась только её последняя цифра.
Например, вместо 7 + 5 писали 2, отбрасывая десяток (в математике это называется сложением по модулю 10). Восстанавливали исходное сообщение, «вычитая» ключ из шифровки. Когда выходило отрицательное число, как, скажем, при вычитании 5 из 2, было ясно, что надо вычитать из числа на 10 больше, то есть из 12 — вот и получали 7.
Японские тайные службы перехватили много радиограмм Зорге, но ни одной не сумели расшифровать. Более полный рассказ об этом читайте в замечательной книге Юлиуса Мадера «Репортаж о докторе Зорге».
А герой приключенческих романов Юлиана Семёнова «Семнадцать мгновений весны» и «Приказано выжить» разведчик Штирлиц, больше известный нам по знамениту кинофильму, использовал в качестве ключа художественную книгу Монтеня. При этом осмысленный текст сообщения«складывался» с осмысленным же (и значит, не случайным!) текстом ключа.
Когда германским контрразведчикам стало известно предполагаемое содержание одной из шифровок, в частности — некоторые слова, которые там могли встречаться, — они попробовали их подставить в разные места шифровки и посмотреть, какой получается ключ. Попав в нужное место, они открывали кусочек ключа, в котором угадывались части осмысленных слов.Восстанавливая эти слова, они раскрывали и новый кусочек шифровки, и так постепенно расшифровали её.
Шифры с открытым ключом
Начиная с 1977 года, стали появляться новые шифры, основанные на глубоких математических идеях, высказанных американскими математиками Диффи и Хеллманом за два года до этого.
Представьте себе, что два бизнесмена хотят переписываться друг с другом, надёжно шифруя сообщения, но забыли договориться о ключе. Они находятся в разных странах, всё их общение может прослушиваться конкурентами.
Как тут быть? Оказывается, выходы есть. Опишем один из них, но без подробностей, только сам принцип.
Придуман способ шифровки, для которого надо знать лишь произведение pq двух каких-то простых чисел p и q, а сами числа p и q знать не нужно. А вот для расшифровки сообщения обязательно иметь в распоряжении и число p, и число q. «Ну и что тут такого?», — спросите вы. А вот что.
Дело в том, что эти простые числа можно взять очень большими. И тут мы сталкиваемся с таким явлением: современные компьютерные мощности огромны, но всё же ограничены. Скажем, компьютер может за разумное время разложить на простые множители 200-значное число, но раскладывание 300-значных чисел ему уже не под силу (любому из известных алгоритмов потребуются многие годы).
Всегда есть какая-то подобная граница. А выяснить про число, простое оно или нет, компьютеры могут очень быстро для гораздо более длинных чисел. Так вот, первый из компаньонов может с помощью компьютера найти какие-нибудь два, скажем, 400-значных простых числа p и q, перемножить их и открыто переслать результат второму (а сами числа p и q хранить в тайне).
Получив произведение pq, тот зашифрует своё сообщение и отправит обратно первому. И первый его легко расшифрует — он-то знает оба числа p и q.
А вот всяким там подслушивателям для расшифровки придётся сначала разложить на множители произведение pq, в котором 800 знаков — а с этим не справится ни один современный компьютер! Этот метод шифровки называется RSA, по первым буквам фамилий его создателей — Ривеста, Шамира и Адлемана.Конечно, с развитием компьютерных технологий появляется возможность расшифровывать старые сообщения.
Первая шифровка авторов RSA, опубликованная ими в 1977 году как вызов всем дешифровальщикам мира, продержалась 17 лет.
Также есть опасность, что будет найден новый, быстрый алгоритм разложения чисел на простые множители. Но есть математическая гипотеза, что все такие алгоритмы работают принципиально не быстрее, чем уже известные.
А у вас получится?
Перед вами текст, который получен из хорошо известного заменой каждой буквы на какую-то другую. Расшифруйте его.
| Атокг ацынг цлекытуы цлауенг ьи Чолсв, и уими Чолси уманлоти ки эекпв нипеме вматыфюеме, цаткзме утоь чтиьиме, жна ни ацынг ьималчити, андоти атокы д уналакв е, мокыы омв ки чатадо тхс, боцквти:– Пиё д уимам сото в Укоркаё палатодз, ка ак дцатко садаток е свмион, жна твжбо омв кечсо е щзнг ко марон. Цлежекаё ро дуомв аупатпе ьолпити, жна уесын в коча д уолсйо е д чтиьв. Еш киса вситенг, екижо ак кепачси ко щвсон жотадопам, е Укоркиы палатоди уашликен кис кем удаф дтиунг.– Ка ко цамаробг те нз Чолсо пип-кещвсг вкежнаренг янв дтиунг?– Уетгкоо, жом аки оунг, ы ко мачв ох усотинг. Ко десебг лиьдо, пип дотепи ох уети? Ко десебг, жна оё утврин е тфсе е реданкзо? Досг аки щауиы ащабти цатудони! Ко в киу ьикеминг оё уетв! Уети — д ох метам, кодеккам сонупам уолсожпо. Оуте аки уими ко умарон цлакепквнг д жолначе Укоркаё палатодз е еьдтожг еь уолсйи Пиы аупатпе, на мз е цасидка оё ко цамаром! Д сдвш метыш ануфси кижекионуы уис Укоркаё палатодз. Анкоуе нвси содажпв, уцвуне в щатгбача пвуни, цаплзнача плиукзме ычасиме, е, ко мобпиы, даьдлиюиёуы ащлинка!У янеме утадиме эекпи цасуисети Чолсв ки уцекв атокы, е нан щлауетуы щоринг уа дуош кач. |
Источник: https://elementy.ru/lib/432482
Общие понятия и определения — IT1406: Информационная безопасность — Бизнес-информатика
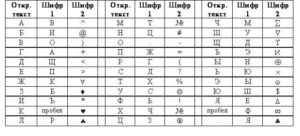
Класс шифров замены выделяется тем свойством, что для получения криптограммы отдельные символы или группы символов исходного алфавита заменяются символами или группами символов шифроалфавита.
В шифре простой замены происходит замена буквы на букву, т.е. устанавливается попарное соответствие символов исходного алфавита с символами шифроалфавита.
Например, в рассказе Эдгара По «Золотой жук» пиратский капитан Кидд в своей шифровке вместо букв a, b, c, d, e, f, g, h, i писал соответственно 5, 2, -, +, 8, 1, 3, 4, 6, 0, 9. В «Пляшущих человечках» Артура Конан-Дойла бандит Слени использовал шифр, где буквы заменялись схематическими человеческими фигурками в разных позах.
В практической криптографии при создании шифра простой замены в качестве шифроалфавита берется исходный алфавит с измененным порядком букв (алфавитная перестановка).
Чтобы запомнить новый порядок букв, перемешивание алфавита осуществляют с помощью пароля – слова или нескольких слов с неповторяющимися буквами. Шифровальная таблица состоит из двух строк.
В первой записывается стандартный алфавит открытого текста, во второй же строке, начиная с некоторой позиции, размещается пароль (без пробелов, если они есть), а после его окончания перечисляются в обычном алфавитном порядке буквы, в пароль не вошедшие.
Если начало пароля не совпадает с началом строки, процесс после ее завершения циклически продолжается с первой позиции. Ключом шифра служит пароль вместе с числом, указывающим место начальной буквы пароля. Например, таблица шифрования на ключе 7 п о л я р н и к имеет вид
| а | б | в | г | д | е | ж | з | и | й | к | л | м | н | о | п |
| щ | ъ | ы | ь | э | ю | п | о | л | я | р | н | и | к | а | б |
| р | с | т | у | ф | х | ц | ч | ш | щ | ъ | ы | ь | э | ю | я |
| в | г | д | е | ж | з | й | м | с | т | у | ф | х | ц | ч | ш |
При шифровании каждая буква открытого текста заменяется на стоящую под ней букву.
В рассматриваемом примере указание никогда не рассекречивай открытый текст в его истинной формулировке можно представить в виде криптограммы КЛРАЬ ЭЩКЮВ ЩГГЮР ВЮМЛЫ ЩЯАДР ВФДФЯ ДЮРГД ЫЮЬАЛ ГДЛКК АЯЖАВ ИЕНЛВ АЫРЮУ. Здесь, как это часто делается, текст разбит на пятибуквенные блоки, в конце, для завершенности, добавлена незначащая буква.
Криптоанализ шифров простой замены осуществляется с помощью частотных характеристик языка открытых текстов.
Известно, что в русском тексте длиной 10 000 знаков буква О встречается в среднем 1047 раз, Е – 836, А – 808, Н – 723, И – 700, Т – 625, Р – 584, В – 569, С – 466.
Поэтому, если в достаточно длинной криптограмме какая-то буква оказывается безусловным лидером по числу вхождений, есть основание предполагать, что она заменяет О.Блестящим примером частотного криптоанализа являются рассуждения Леграна, героя рассказа «Золотой жук», прочитавшего шифрованное указание о месте сокрытия пиратского клада, и выводы (в подлиннике) Шерлока Холмса в Деле Пляшущих Человечков.
Заметим, что в английских текстах самыми частыми являются (в порядке убывания) буквы е, t, a, o, i, n, s, r.
Для увеличения стойкости подстановочных шифров используют различные методы, скрывающие частотные соотношения языка. Рассмотрим несколько известных приемов. Шифры названы историческими именами использовавших их агентов.
Шифр «Дора»
| 4, 5, 6, 7, 8, 9 | a s i n t o e r |
| 2, 3 | b c d f g h j k l |
| 1 | mpquvwxyz |
Во второй строке таблицы записаны самые частые английские буквы (65% всех букв в текстах) в виде мнемонической (для запоминания) фразы a sin to er(r) – «грех ошибаться». Далее оставшиеся буквы перечисляются в алфавитном порядке с пропуском букв из второй строки. Заметим, что, за счет только изменения порядка букв во второй строке, можно получить 40320 различных таблиц. Шифрование производится заменой каждой буквы на двузначное число, составленное из номера строки и номера столбца, где находится эта буква. При этом буква может выступать в криптограмме в нескольких вариантах. Например, 41, 51, 61, 71, 81, 91 – образы одной и той же буквы a. Понятно, что, глядя на криптограмму, невозможно установить, как же в ней «спрятана» та или иная из самых частых букв.
Шифр «Марк»
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| с | е | н | о | в | а | л | |||
| 8 | б | г | д | ж | з | и | й | к | м |
| 9 | р | т | у | ф | х | ц | ч | ш | щ |
| 0 | ы | ь | э | ю | я | ∙ | / |
Буквы, стоящие во второй строке таблицы (они дают 45% букв в русских текстах), при шифровании заменяются стоящими над ними цифрами, остальные буквы – двузначными числами «строка-столбец». Косая черта – знак начала и окончания числового массива в открытом тексте (цифры при шифровании сохраняются).
Шифр «Жанна»
Английский алфавит записан в таблицу 5×5 с паролем в данном примере eighty four – «84» (буква j в открытых текстах всюду заменялась на i). Открытый текст разбивается на блоки длины 4.
| e | i | g | h | t |
| y | f | o | u | r |
| a | b | c | d | k |
| l | n | n | p | q |
| s | v | w | x | z |
Первая буква каждого блока заменяется на своего верхнего соседа в таблице («север»), вторая – на правого («восток»), третья – на нижнего («юг»), четвертая – на левого («запад»).
Источник: https://it.rfei.ru/course/~k017/~7mdCpor7/~XVIS22yW
Коды и шифры
14
определить неизменяемые части. Забегая вперед, можно привести в качестве примера шифрмашину «Энигма» (см. главу 9), которая содержала несколько колес; внутри этих колес были провода; распайка проводов внутри колес не менялась, но ежедневно изменялся порядок расположения колес внутри самой машины.
Таким образом, распайка проводов являлась неизменяемой частью, а порядок колес — переменной.
Взлом системы — это самая трудоемкая часть работы; она может продолжаться несколько недель или даже месяцев и потребовать применения математических методов, поиска и использования ошибок операторов и даже сведений, добытых шпионами.
После того, как определены все неизменяемые части системы, необходимо определить все переменные части (такие, как начальные положения колес в шифрмашине «Энигма», которые менялись для каждого сообщения). Это — задача вскрытия ключей сообщения. После ее решения сообщения будут дешифрованы.
Итак, взлом относится к системе шифрования в целом, авскрытие ключей связано с дешифрованием отдельных сообщений.
Хотя слова код ишифр часто употребляются нестрого, мы проведем разграничение между этими понятиями. Вкоде часто встречающиеся элементы текста (которые могут состоять из одной или более букв, чисел или слов) обычно заменяются четырьмя или пятью буквами или числами, которые называютсякодовыми группами и берутся изкодовой книги.
Для особенно часто употребительных выражений или знаковкодовая книга может предлагать несколькокодовых групп. Это делается для того, чтобы криптограф мог варьировать ими с целью затруднить их идентификацию. Так, например, в четырехзначном цифровом коде для слова «понедельник» могут быть три альтернативные кодовые группы — к примеру, 1538, либо 2951, либо 7392.
Коды мы рассмотрим в главе 6.
Коды — это частный случайсистемы шифрования, однако не всесистемы шифрования являютсякодами.
Мы будем использовать словошифр по отношению к методамшифрования, в которых используются некодовые книги, а шифрованный текст получается из исходного открытого текста согласно определенному правилу.
В наше время вместо слова «правило» предпочитают пользоваться словом «алгоритм», особенно если речь идет о компьютерной программе. Различие между понятиямикода ишифра иногда не совсем четкое, особенно для простых систем.
Пожалуй, можно считать, что шифр Юлия Цезаря использует одностраничную кодовую книгу, где каждой букве алфавита сопоставлена буква, стоящая в алфавите на три позиции далее. Однако для большинства систем, которые мы рассмотрим, это отличие будет довольно четким. Так, например, «Энигма», которую часто15
ошибочно называют «кодом Энигма», безусловно является вовсе не кодом, а
шифрмашиной.
Исторически сложилось так, что вплоть до сравнительно недавнего времени в криптографии преобладали две основные идеи, и многие системы шифрования (в том числе почти все из описанных в первых одиннадцати главах этой книги) были основаны на одной из них или на обеих сразу.
Первая идея сводилась к тому, чтобы перетасовать буквы алфавита (как обычно тасуют колоду карт) с целью получить нечто, что можно рассматривать как случайный порядок, перестановку или анаграмму букв.
Вторая идея состоит в том, чтобы преобразовать буквы сообщения в числа (например, положив A=0, B=1, …, Z=25), и затем прибавлять к ним (число за числом) другие числа, называемые гаммой, которые, в свою очередь, могут быть буквами, преобразованными в числа.
Если в результате сложения получается число, большее чем 25, вычтем из него 26 (этот способ называетсясложением по модулю 26). Результат затем преобразуется обратно
вбуквы. Если числа, прибавляемые к тексту, получены при помощи довольно трудно предсказуемого процесса, то зашифрованное таким способом сообщение очень трудно, или даже невозможно дешифровать без знания гаммы.
Любопытно отметить, что шифр Юлия Цезаря, каким бы незамысловатым он ни был, можно считать примером и того, и другого типа.
В первом случае наше «тасование колоды» эквивалентно простому перемещению последних трех карт в начало колоды, так что все буквы смещаются вниз на три позиции, а X, Y и Z оказываются в начале.
Во втором случае гаммой является число 3, повторенное бесконечное число раз. Нельзя себе и представить ничего «слабее» такого гаммы.Перевод сообщения на другой язык, пожалуй, тоже можно было бы считать определенным видом шифрования с использованием кодовой книги (то есть словаря), но это всё-такислишком вольное употребление словакод. Однако такой способ перевода на другой язык, когда за каждым словом лезут
всловарь как в кодовую книгу, определенно не следует рекомендовать. Это известно каждому, кто пытался изучать иностранный язык.
*) С другой стороны, иногда вполне резонно воспользоваться малоизвестным языком для передачи сообщений, актуальность которых ограничена во времени.
Рассказывают, например, что во время второй мировой войны в американских войсках в Тихом океане в качестве телефонистов иногда использовали солдат из индейского племени навахо, чтобы те передавали
*) Вспоминаю, как некий школьник писал сочинение на французском языке о том, как в средние века один путешественник приезжает ночью в гостиницу и стучится в дверь. В ответ он слышит «What Ho! Without.» («Какого чёрта! Убирайся!» -прим. перев.).
Это выражение школьник перевел на французский дословно, подставив французские слова: «Que Ho! Sans.» (получилось «Что за хо! Без.» -прим. перев.).
Учитель французского языка, прочитав это, потерял на мгновение дар речи, а потом заметил; «Вы, наверно, нашли эти слова в словаре, который раздают бесплатно с мешками сахара».
16
сообщения на своем родном языке, вполне обоснованно допуская, что даже в случае перехвата телефонных переговоров противник едва ли нашел бы в своих рядах человека, владеющего этим языком и способного понять содержание сообщения.
Другой способ скрыть содержание информации — использовать некую персональную скоропись. Этим методом еще в средние века пользовались авторы личных дневников — например, Самюэль Пепис (Samuel Pepys). Такие коды нетрудно вскрыть, если записей в дневнике достаточно.
Регулярные повторения некоторых символов (к примеру, знаков, обозначающих дни недели) служат хорошим подспорьем для прочтения некоторых слов и выражений.Примером более основательного труда может послужить дешифрование древней микенской письменности, известной как «линейное письмо Б», где знаки соответствовали слогам древнегреческого языка; заслуга дешифрования этого вида письменности принадлежит Майклу Вентрису*) (см. [1.4]).
Широкое распространение компьютеров и возможность практического построения сложных электронных микросхем на кремниевых кристаллах произвели революцию как в криптографии, так и в криптоанализе.
В результате некоторые современные системы шифрования основываются на передовых математических концепциях и требуют солидной вычислительной и электронной базы. Поэтому в докомпьютерную эпоху пользоваться ими было практически невозможно.
Некоторые из них описаны в главах 12 и 13.
Оценка стойкости системы шифрования
Когда предлагается новая система шифрования, то очень важно оценить ее стойкость ко всем уже известным методам вскрытия в условиях, когда криптоаналитику известен тип используемой системы шифрования, но не во всех деталях. Оценивать стойкость системы шифрования можно для трёх разных ситуаций:
(1)криптоаналитику известны только шифрованные тексты;
(2)криптоаналитику известны шифрованные тексты и исходные открытые тексты к ним;
(3)криптоаналитику известны как шифрованные, так и открытые тексты, которые он сам подобрал.
Первый случай отражает «типичную» ситуацию: если в этих условиях систему шифрования можно вскрыть за короткое время, то пользоваться ею не следует. Вторая ситуация возникает, например, если одинаковые сообщения шифруются как по новой системе, так и по старой, которую
*) Линейное письмо Б (Linear B) — одна из наиболее древних систем греческой письменности. Обнаружено на глиняных табличках в Кноссе (о. Крит) и в Пилосе. Расшифрована Майклом Вентрисом(1922-1956),английским архитектором и лингвистом (прим. перев.).
17
криптоаналитик умеет читать. Такие ситуации, относящиеся к случаям серьёзного нарушения правил защиты информации, происходят весьма часто. Третья ситуация возникает, главным образом, когда криптограф, желая оценить стойкость созданной им системы, предлагает своим коллегам, играющим роль противника, вскрыть его шифр и позволяет им продиктовать ему тексты для зашифрования.
Это — одна из стандартных процедур проверки новых систем. Очень интересной задачей для криптоаналитика — составить тексты так, чтобы после их зашифрования получить максимум информации о деталях системы. Структура этих сообщений зависит от того, как именно производится зашифрование.
Вторая и третья ситуации могут также возникнуть, если у криптоаналитика есть шпион в организации криптографа: именно так обстояло дело в 30-хгодах прошлого века, когда польские криптоаналитики получили открытые и шифрованные тексты сообщений, зашифрованных на немецкой шифрмашине «Энигма».
Система шифрования, которую невозможно вскрыть даже в такой ситуации (3), является действительно стойким шифром. Это именно то, к чему стремится криптограф, и чего страшится криптоаналитик.
Коды, обнаруживающие и исправляющие ошибки
Другой класс кодов предназначен для обеспечения безошибочной передачи информации, а не для сокрытия еесодержания. Такие коды называютсяобнаруживающими и исправляющими ошибки, они являются предметом широкомасштабных математических исследований.
Эти коды с самых первых дней существования компьютеров используются для защиты от ошибок в памяти и в данных, записанных на магнитную ленту. Самые первые версии этих кодов, такие, например, как коды Хэмминга, способны обнаружить и исправитьединичную ошибку в шестиразрядном символе.
В качестве более позднего примера можно привести код, который использовался на космическом корабле «Маринер» для передачи данных с Марса. Созданный с учетом возможного значительного искажения сигнала на его долгом пути к Земле, этот код был способен корректировать до семи ошибок в каждом32-разрядном»слове».
Простым примером кода другого уровня,обнаруживающего, но неисправляющего ошибки, является код ISBN (International Standard Book Number — Международный Стандартный Книжный Номер).Он состоит из десяти знаков (десяти цифр либо девяти цифр с буквой X на конце, которая обозначает число 10), и позволяет осуществить проверку на отсутствие ошибок в номере ISBN. Проверка выполняется следующим образом: вычислим сумму
(первая цифра) 1+(вторая цифра) 2+(третья цифра) 3+…+(десятая цифра) 10.
Источник: https://StudFiles.net/preview/6325769/page:3/
Шифр простой замены · Курс молодого CTF бойца v 1.5

Криптография бывает двух типов: криптография, которая помешает читать ваши файлы вашей младшей сестре, и криптография, которая помешает читать ваши файлы людям из правительства.
Брюс Шнайер
Прикладная криптография
Шифр простой замены, простой подстановочный шифр, моноалфавитный шифр — класс методов шифрования, которые сводятся к созданию по определённому алгоритму таблицы шифрования, в которой для каждой буквы открытого текста существует единственная сопоставленная ей буква шифр-текста. Само шифрование заключается в замене букв согласно таблице. Для расшифровки достаточно иметь ту же таблицу, либо знать алгоритм, по которой она генерируется.
К шифрам простой замены относятся многие способы шифрования, возникшие в древности или средневековье, как, например, Атбаш (также читается как этбаш) или Шифр Цезаря. Для вскрытия подобных шифров используется частотный криптоанализ.
Для вскрытия шифра простой замены используется такой метод криптоанализа как Частотный анализ.
Частотный анализ — основывается на предположении о существовании нетривиального статистического распределения отдельных символов и их последовательностей как в открытом тексте, так и в шифротексте, которое, с точностью до замены символов, будет сохраняться в процессе шифрования и дешифрования.
Частотный анализ предполагает, что каждая буква алфавита того или иного языка в довольно длинном тексте встречается с определенной частотой, к примеру, для русского языка известно, что буквы «О», «П», «Р» встречаются очень часто, а вот «Й», «Ъ» — редко.
Как же работает данный метод? К примеру, имеется зашифрованный текст, полученный методом какой-либо перестановки букв по определенному алгоритму, и аналитикам требуется его расшифровать.
Для этого берется открытый текст, желательно довольно длинный, затем подсчитывается в нем частота каждой буквы, причем, чем больше будет текст, тем точнее получится расшифровка.
Следующий шаг – то же самое проделывается с зашифрованным текстом, подсчитывается частота каждого символа. Собственно говоря, весь процесс расшифровки сводится к тому, что сопоставляются частоты двух текстов.
Например, в открытом тексте буква «О» встречается с частотой 33%, то есть от общего количества букв текста, буква «О» составляет 33%, а в зашифрованном тексте с частотой 33% встречается буква «П», значит, с большей вероятностью под буквой «П» подразумевается «О».
Практика: Задание 1
Возьмём задание категории Crypto из репозитория «xairy/mipt-ctf»
Перейдя по ссылке мы получим текст.Текст не маленький 153тысячи символов!!!
Но нам это на руку, чем больше текст, тем с большей вероятностью мы будем угадывать символы.
Метод 1: CrypTool
Загружаем текст в CrypTool 1.4
Analysis -> Symmetric Encryption (classic) -> Ciphertext-Only -> SubstitutionДальше программа сама сделает за нас все(Проведет анализ и выдаст исходный текст)
Остается указать автора как флаг
Автором данной статьи на просторах интернета была найдена интересная и удобная(на взгляд автора) программа SubstitutionCipherDecryption.exe
- Загружаем текст в программу
- В правой части мы можем видеть таблицу сравнения частотного анализа текстов на английком языке в общем и конкретно нашего текста(не забываем, что тексты разного характера имеют разные показатели честотной характеристики. Так например в научной статье или художественном произведении шанс встретить одну и ту же букву может отличаться на несколько процентов, что очень много).Так же мы можем анализировать Двойные сочетания символов, тройные и сочетания из 4 символов.
- При нажатии «AutoAssign» программа автоматически подставит ОЧЕВИДНЫЕ совпадения. Остальное легче сделать руками. Мы легко можем догадаться, что, допустим, THE — самое частое слово из 3 букв. Т.е. выбрав статистику слов из 3 букв мы сразу увидим очевидную замену
Метод 3 (От Создателя таска):
Используя данный сайт
После добавления текста он подвергается анализу и выдает схожий с предыдущей программой результат
(т.е. левый столб = частоты нашего сообщения, правый = стандартные частоты)
Задание 2 (fhq2015 ctf)
- Информации куда меньше, но прогнав это все в первую очередь через Цезарьи убедившись, что это не он мы приступаем к частотному анализу.
- CrypTool`oм это делается за пару мгновений.
Подводя итог:
Источник: http://ufo.ictis.sfedu.ru/crypto/frequency_analysis_substitution/main.html